Белорусский государственный университет информатики и радиоэлектроники г. Минск, Республика Беларусь

Абражевич Д.С.

В работе представлена методика топологической оптимизации композитных структур несущих конструкций радиоэлектронных средств. Подтверждение адекватности разработанной методики осуществлено посредством создания проекта оптимизации в программном комплексе ANSYS Workbench.

Специфика композитной структуры как объекта оптимизации состоит в следующем. Во-первых, технологические особенности строения многослойных композитов, составленных, как правило, из монослоев фиксированной толщины, определяют дискретную природу ряда задач оптимизации их параметров и структуры. Однако в большом числе работ эти задачи ставятся и решаются в непрерывной постановке. Во-вторых, многомерность пространства проектных параметров усложняет поиск глобального экстремума целевого функционала. Успешное решение такой задачи требует применения адекватной методики оптимизации.

Анализ литературы показал, что практически нет работ по компьютерному моделированию топологической оптимизации конструкций из слоистых композиционных материалов. Небольшое количество работ объясняется не отсутствием интереса к этим проблемам, а существенными трудностями, связанными с построением алгоритма расчёта с помощью интегрированных систем CAE.

Для решения такого класса задач в работе сделана попытка разработать методику оптимизационного расчёта, которая предусматривает все этапы решения, начиная с постановки задачи, построения модели, решения и анализа результатов. На Рисунок 1 приведены основные этапы расчёта.

На первом этапе (препроцессорная подготовка) выполняется построение и отображение геометрической модели рассчитываемого изделия, а также осуществляется построение конечно-элементной сетки.

Следующим шагом идет создание имитационной модели слоистых композиционных материалов. На данном этапе осуществляется настройка материалов, задание характеристик слоев, а также направление их укладки. В результате организуется расчетная композитная структура.

Далее описанные выше характеристики преобразуются в параметры для их использования во время оптимизационной подзадачи.

Следующий этап – решение конечно-элементной задачи, которое включает задание вида анализа и его опций, нагрузок, шага решения и заканчивается запуском на счёт. В случае сходимости решателя мы преобразуем полученные характеристики в параметры для их дальнейшего использования в качестве целевых функций.

После чего мы переходим к решению оптимизационной подзадачи. На данном шаге мы ограничиваем наши параметры и описываем целевые функции. После чего запускается оптимизационный расчет.

На этапе пост-обработки результатов мы анализируем полученные значения целевых функций и отсеиваем не подходящие итерации.

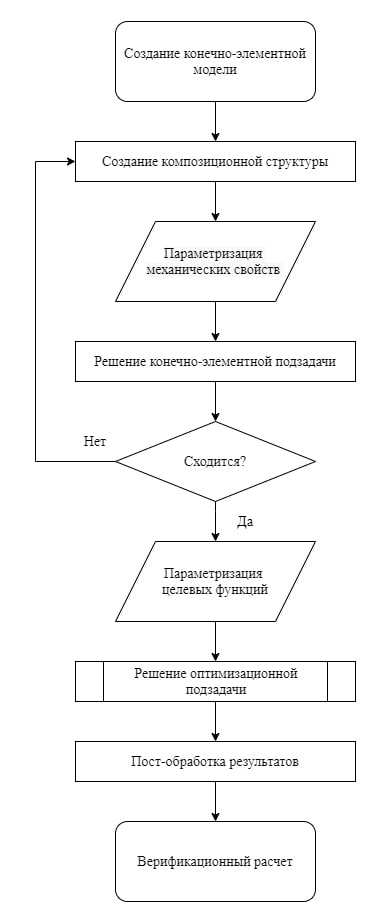
Рисунок 1 – Методика оптимизации композитной структуры

В конце необходимо провести верификационный расчет и повторно проанализировать результаты. Итогом работы программы является графическое и табличное представление результатов.

Для подтверждения адекватности разработанной методики осуществим топологическую оптимизации трехслойной крышки радиоэлектронного средства (рисунок 2) в программном комплексе ANSYS Workbench.

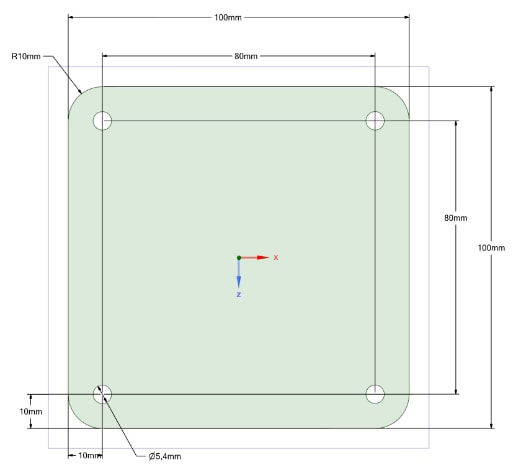
Рисунок 2 – Геометрическая модель крышки

Структура проекта изображена на Рисунок 3. Блок «A» отвечает за построение геометрии. Блок «B» осуществляет построение конечно-элементной сетки и создает имитационную модель слоистой композиционной структуры. Блок «С» реализует решение конечно-элементной задачи. Блок «D» выполняет визуальную пост-обработку результатов. Блоки «E» и «F» являются копиями блоков «B» и «С», соответственно, с добавлением твердотельной композиционной структурой. Твердотельная модель в дальнейшем используется в блоке «G» для структурной оптимизации. Данные три блока дополнительно служат верификационным расчет, полученных данных при параметрической оптимизации. Блоки «H», «I» и «J» являются модулями оптимизации параметров композиционной конструкции. Каждый из блоков служит для определенной итерации оптимизации, таким образом удается обойти ситуацию, когда толщина слоев может равняться нулю.

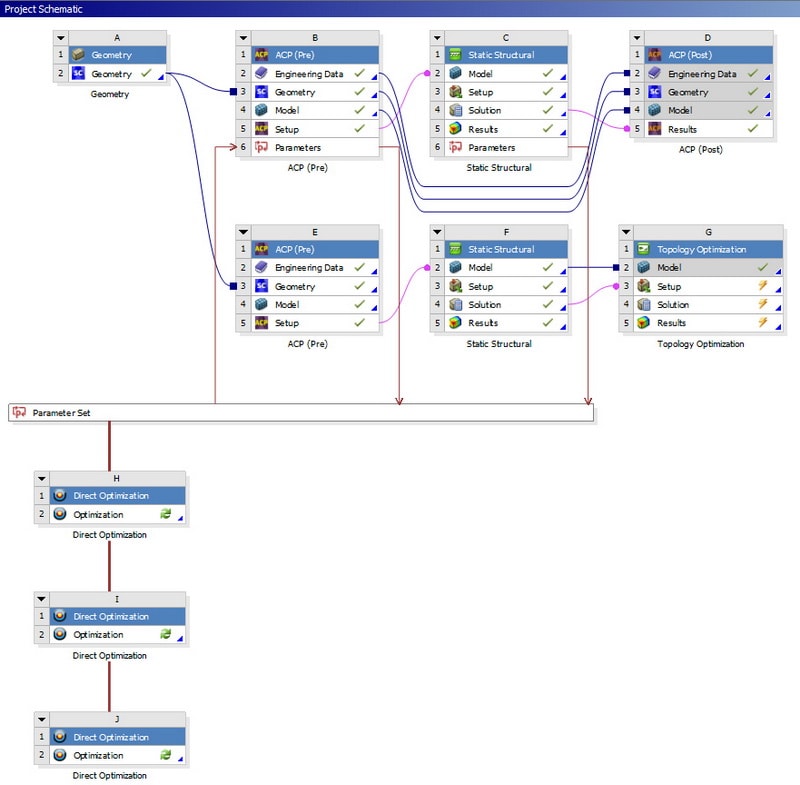
Рисунок 3 – Структура проекта в програмном комплексе ANSYS Workbench

Для того, чтобы провести параметрическую оптимизацию необходимо задать параметры для каждого слоя. Параметрами могут выступать любое значение, введенное пользователем во время построения модели. Исходя из исходных данных нам необходимо задать семь параметров, а именно толщину и угол укладки каждого слоя, и вес конечного изделия.

В блоке «B» с помощью команды «Create Parameter» зададим параметр толщины слоя. Для того, чтобы параметр можно было менять в дальнейшем расчете в пункте «Category» необходимо поставить значение «Input». В пункте «Object» зададим нашу первую ткань, а в пункте «Property» выберем толщину. Значение переменной отобразиться в пункте «Value». Тоже самое проделаем и для создания параметра угла укладки, но в пункте «Object» зададим уже смоделированный слой, а в пункте «Property» выберем угол слоя. Параметр веса является целевой функцией и получается при моделировании конструкции, поэтому при его задании как параметра необходимо учитывать следующие особенности: в пункте «Category» необходимо поставить значение «Output , в пункте «Object» зададим наш «Sensor», а в пункте «Property» выберем вес. Таким образом была создана параметрическая композитная структура, которую дальше можно использовать для статических и динамических расчетов.

За параметрическую часть оптимизации отвечают три блока: «H», «I», «J». Это обусловлено тем, что каждый блок отвечает за свою собственную комбинацию слоев, таким образом удается избежать ошибки оптимизации при толщинах слоя равных нулю. Перейдем к рассмотрению настроек оптимизации.

В первую очередь во вкладке «Optimization» необходимо выбрать метод оптимизации. Исходя из анализа приведенном в статье [1] был выбран метод Adaptive Multiple-Objective.

Следующим шагом необходимо описать целевые функции. Во вкладке «Objectives and Constrains» задаются целевые функции оптимизации, а также их возможные ограничения. Исходя из поставленных задач зададим следующие целевые функции (Рисунок ):

• F1: масса, тип – минимизировать, цель – 0 кг, ограничение – поиск значений меньше 0,0439, точность – 0,001;
• F2: запас прочности, тип – минимизировать, цель – 0, ограничение – поиск значений меньше 1, точность – 0,001.

Рисунок 4 – Целевые функции

Во вкладке «Domain» перечисляются все параметры, имеющие статус «Input». В блоке «H» будут рассчитаны все возможные комбинации построения для одного слоя, в блоке «I» – для двух слоев, в блоке «J» – для трех, соответственно. Не нужные в расчете параметры отключаются путем снятия галочки с поля «Enable».

Далее зададим граничные условия параметров толщины и угла укладки. Эти параметры следует задавать из технических возможностей оборудования. В настройках параметра «Ply tickness» зададим нижнюю границу 0,0005м, а верхнюю 0,002м. Тип допустимых значений (англ «allowed values») зададим как привязка по шагу (англ «snap to grid») – шаг составит 0,0005м. Те же действия повторим и для параметра «Ply angel», интервал значений от -45° до 90° с шагом 45°. Таким образом обеспечиваются все возможные комбинации толщин слоев и их возможных укладок.

Во вкладке «Raw Optimization Data» представлены комбинации параметров, которые удовлетворяют заданным расчетным ограничениям. Во вкладке «Results» будут отображены только лучшие возможные комбинации заданных параметров.

В результате параметрической оптимизации было получено, что, если изделие изготовить из одного слоя композита, толщиной 0,002м и углом укладки 90°, то конструкция может получиться в 3 раза прочнее, чем предполагалось изначально. А конструкция, состоящая из двух слоев, уже может иметь хороший запас прочности и быть легче изначальной конструкции. Отсюда можно сделать вывод, что всегда следует рассматривать все возможные варианты оптимизации.

Получив лучшие комбинации параметров при параметрической оптимизации, перейдем к топологической оптимизации несущей конструкции. В качестве примера выберем комбинацию, когда у нас есть два слоя толщиной 0,005м и 0,002м, с углами укладки -45° и 90° соответственно.

Полученные расчетные данные из ячейки «Solution» блока «F» импортируем в ячейку «Setup» блока «G». В окне настройки области оптимизации зададим все тело, однако исключим из расчета отверстия и первый слой КС, который будет опираться на корпус. В качестве оптимизационного решателя зададим метод «Density Based». В окне «Response constraints» целью оптимизации зададим сохранение 75% массы (англ. Mass) от стартовой массы изделия.

Результаты топологической оптимизации представлены на Рисунок . Итоговая масса составила 0,0294 кг.

Рисунок 5 – Оптимизированная конструкция

Благодаря разработанной методике топологической оптимизации композитных структур несущих конструкций радиоэлектронных средств было осуществлено уменьшение веса исходного изделия на 67% и увеличение прочности конструкции на 510%, с уменьшением общей толщины конструкции на 0,0005м.

Список использованных источников:

1. Абражевич Д.С. Системы исследования параметрической оптимизации в ANSYS Workbench // Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ: сб. ст. по мат. XC междунар. студ. науч.-практ. конф. № 6(89). URL: https://sibac.info/archive/technic/6(89).pdf.

2. Боровков, А. И. Компьютерный инжиниринг [Текст]: учебное пособие – СПб.: Изд-во СПбПУ, 2012. – 93 с.

3. Конотоп, Д.И. Оптимальное проектирование сложных технических объектов с использованием онтологического подхода / Д. И. Конотоп, В. П. Зинченко//Онтология проектирования, 1(2), 2011, с. 44-53

4. Болдырев, А. В. Методика обучения топологическому проектированию конструкций на основе моделей тела переменной плотности. / А. В. Боды- рев, М. В. Павельчук // Онтология проектирования – 2016 – Т.6, № 4 (22). С. 501 -513.

5. Черняев А.В. Критерии прочности композитных материалов [Электронный ресурс] : М-во образования и науки Рос. Федерации, Самар. гос. аэрокосм. ун-т им. С. П. Королева (нац. исслед. ун-т) (СГАУ) – 2014. – 56 с.

6. Муйземнек А.Ю., Карташова Е.Д. Механика деформирования и разрушения полимерных слоистых композиционных материалов: учебное пособие. – Пенза: Изд-во ПГУ, 2017. – 77 с.